A heap is a special type of tree like data structure that will always provide the maximum or minimum value at the root depending on the type of heap. We will cover all about heap data structure in this article. Before going into the details of heap data structure, let us quickly go over the basic concepts of a binary tree and its array representation.

Binary TreeLink to heading

A binary tree is a tree data structure in which each node has at most two child nodes.

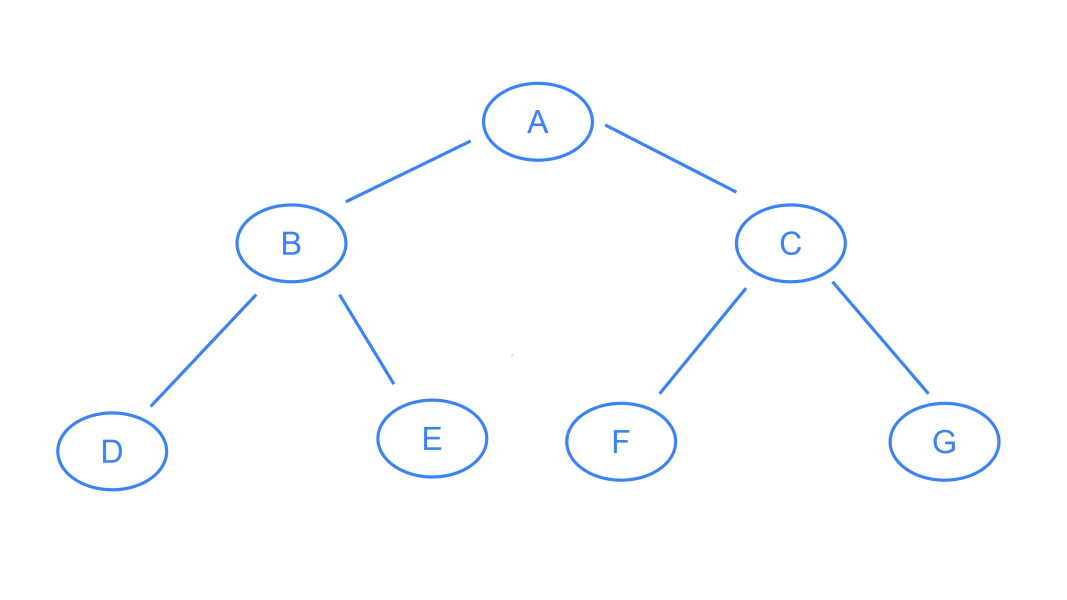
Array Representation of Binary TreeLink to heading

We can easily visualize the binary tree as an array. The array representation of a binary tree must follow the following rules:

1. The root node must be at index 0.
2. The left child of a node must be at index 2 * i + 1.
3. The right child of a node must be at index 2 * i + 2.
4. The parent of a node must be at index floor((i - 1) / 2).

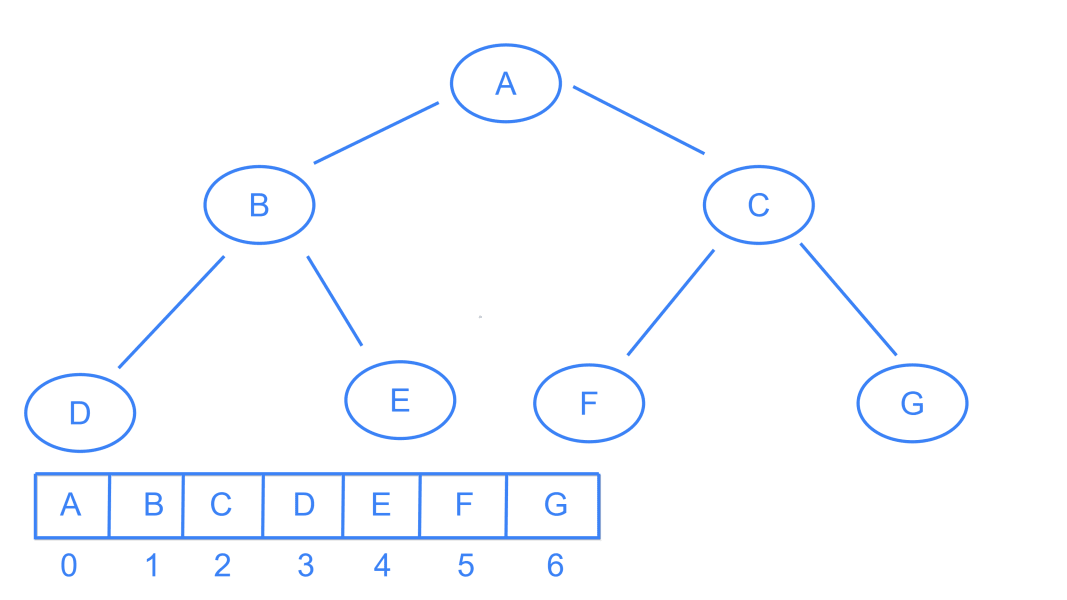
Even if a node is not present in the binary tree, it must follow the above-mentioned rules. For example, in case of below a tree, the child of node B is not present. So, the array representation of the tree must be:

Perfect Binary TreeLink to heading

A perfect binary tree is a binary tree with the maximum number of nodes at each level.

Complete Binary TreeLink to heading

If you represent a binary tree as an array, then there shouldn’t be any empty gaps in between the first and last elements. Every perfect binary tree is also a complete binary tree. A complete binary tree is a full binary tree up to height = height - 1. Height of a complete binary tree will always be equal to log(n)

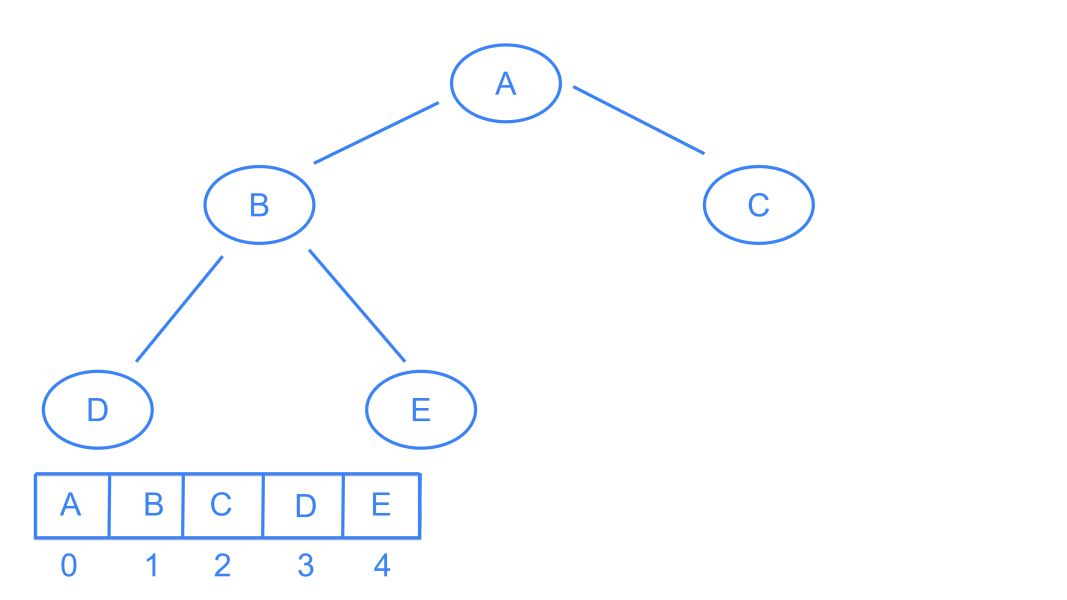
HeapsLink to heading

A heap is a complete binary tree. There are two types of heaps:

1. Max Heap
2. Min Heap

Max HeapLink to heading

A max heap is a complete binary tree in which every node is having a value greater than or equal to all its descendants.

Min HeapLink to heading

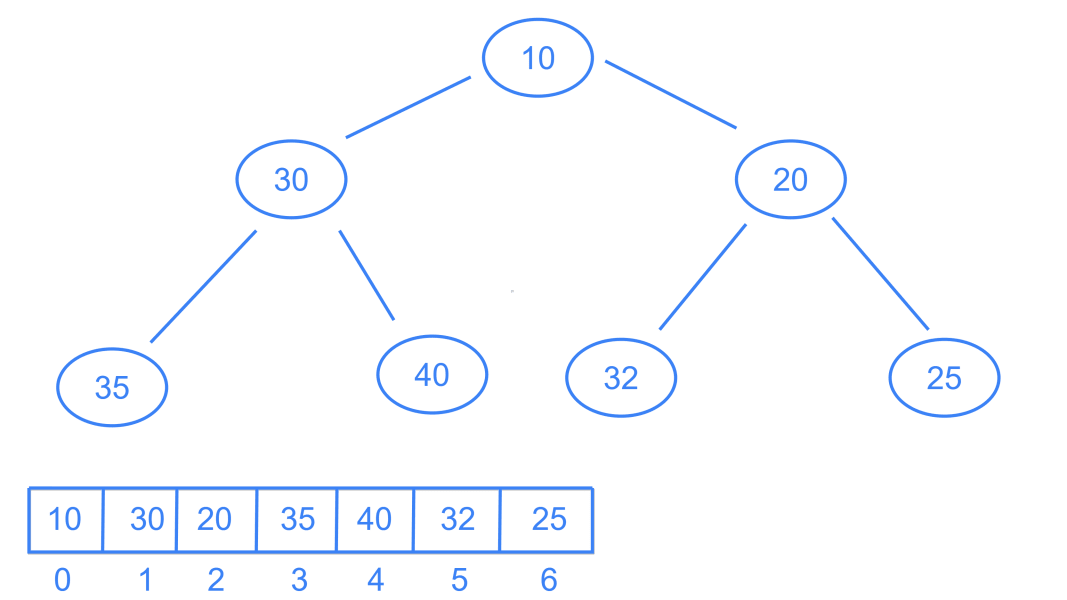
Min heap is a complete binary tree in which every node is having a value less than or equal to all its descendants.

Insertion in HeapLink to heading

To insert a new element in a heap, we need to add it as the last element in the array and move it upwards until it satisfies the heap property. The main thing to notice is that the adjustment is done from the last element to the root. Here is the code to insert a new element in a heap, we are considering it to be a max heap.

1void Heap::insert(int value) {
2    // a complete binary tree with one node is always a binary tree
3    if (size == 0)
4        heap[size++] = value;
5    else {
6        // add element to the leaf
7        heap[size++] = value;
8        // get the index of last item
9        int index = size - 1;
10        // get the parent index
11        int parent = (int) index / 2;
12        // push the value upwards till it satisfies heap property
13        while (index > 0 && heap[parent] < heap[index]) {
14            swap(heap[parent], heap[index]);
15            index = parent;
16            parent = (int) index / 2;
17        }
18    }
19}
20
21// time complexity: O(log n)

Deletion in HeapLink to heading

We can't delete any random element from the heap. We can only delete the root node. After deleting the root node, we need to move the last element in the heap to the root and then move it downwards until it satisfies the heap property. The main thing to notice is that the adjustment is done from root towards the leaf. Here is the code to delete root in a heap, we are considering it to be a max heap.

1void Heap::heapify(int index) {
2    int leftChildIndex = index * 1 + 1;
3    int rightChildIndex = index * 1 + 2;
4    int maxChildIndex = index;
5
6    if (leftChildIndex < size && heap[leftChildIndex] > heap[maxChildIndex]) {
7        maxChildIndex = leftChildIndex;
8    }
9
10    if (rightChildIndex < size && heap[rightChildIndex] > heap[maxChildIndex]) {
11        maxChildIndex = rightChildIndex;
12    }
13
14    if (maxChildIndex != index) {
15        swap(heap[maxChildIndex], heap[index]);
16        heapify(maxChildIndex);
17    }
18}
19
20int Heap::pop() {
21    if (size > 0) {
22        int poppedElement = heap[0];
23        heap[0] = heap[size - 1];
24        size--;
25        heapify(0);
26        return poppedElement;
27    }
28    return -1;
29}
30
31// time complexity: O(log n)

In max heap, whenever we delete an element, we get the largest element. We can keep the deleted elements in the free space in the array. So, after deleting all the elements, we will get the sorted array. This is the idea behind the heap sort.

In heap sort, we first construct a min/max heap and then extract the root node until the heap is empty. The overall time complexity of heap sort is the Creation of heap O(n log n) + Deletion of all elements O(n log n) which is just O(n log n). We can also construct a min/max heap using the heapify algorithm which will only take O(n) time if the array is readily available. This algorithm is mentioned below.

HeapifyLink to heading

In traditional approach, we add elements to the leaf and adjust it upwards, but in heapify the direction is opposite, i.e., we adjust the element downwards. Here is the code to heapify a single node.

1void Heap::heapify(int index) {
2    int leftChildIndex = index * 1 + 1;
3    int rightChildIndex = index * 1 + 2;
4    int maxChildIndex = index;
5
6    if (leftChildIndex < size && heap[leftChildIndex] > heap[maxChildIndex]) {
7        maxChildIndex = leftChildIndex;
8    }
9
10    if (rightChildIndex < size && heap[rightChildIndex] > heap[maxChildIndex]) {
11        maxChildIndex = rightChildIndex;
12    }
13
14    if (maxChildIndex != index) {
15        swap(heap[maxChildIndex], heap[index]);
16        heapify(maxChildIndex);
17    }
18}

We can also use heapify algorithm to create a new heap. We start from the leaf node and maintain the heap property by sending the elements downwards.

1void Heap::constructHeap(const vector<int> &values) {
2    if (size == 0) {
3        for (int value: values) {
4            heap[size++] = value;
5        }
6        for (int i = size - 1; i >= 0; i--) {
7            heapify(i);
8        }
9    }
10}

Heapify algorithm is able to create a heap in O(n) time, whereas traditional approach takes O(n log n) time for n elements. We should always use heapify if the array is readily available.

Priority QueueLink to heading

A priority queue is a special kind of data structure that will always pop the value with the highest priority. We can easily achieve this using a max/max heap. We can also create a priority queue by storing the elements in a normal array, but this will not be efficient as the pop method will take O(n) time.

To make efficient priority queue, we can use a min/max heap. This will return the highest priority element in just O(log n) time, but this will also take O(log n) time for each push, whereas this will take constant time in case of a normal array. So we should always choose the method which is more efficient for our use case.

Quick RecapLink to heading

1. A heap is a complete binary tree with a maximum height of log n.
2. A heap can be a max heap or a min heap.
3. A max heap is a heap in which every node is greater than or equal to its descendants.
4. A min heap is a heap in which every node is less than or equal to its descendants.
5. We can insert a new element in the heap by adding it to the end of the array and then moving it upwards until it satisfies the heap property.
6. We can't delete any random element from the heap except the root node.
7. We can delete the root node by replacing it with the last element and then moving it downwards until it satisfies the heap property.
8. Time complexity of insertion and deletion in heap is O(log n).
9. In heap sort, we first construct a min/max heap and then extract the root node until the heap is empty. This will give us the sorted array in O(n log) time.
10. We can also construct a min/max heap using the heapify algorithm which will only take O(n) time if the array is readily available.
11. Heaps are used to implement efficient priority queues.